Las formas del relieve en Topografía
La Topografía (del griego τόπος, ‘lugar’, y «-grafía», ‘descripción’) como ciencia que estudia la representación gráfica de la superficie terrestre, con sus formas y detalles, tiene como objetivo principal el estudio del relieve. El relieve es el conjunto de formas de la superficie terrestre que resalta sobre una superficie horizontal. Etimológicamente, la palabra proviene del latín relevare, cuya traducción es ‘levantar’, ‘alzar’.
Las formas de relieve, básicamente se pueden clasifican en formaciones montañosas, llanuras y depresiones, y su génesis y evolución responden a la acción del clima, los procesos geológicos internos y externos y las acciones antrópicas.
Se llama superficie topográfica a aquella que envuelve la parte sólida de la Tierra. Aunque considerada en pequeñas zonas puede compararse con planos, conos o cilindros, esta superficie es absolutamente irregular. Su única propiedad geométrica regular es la que se refiere a que una recta vertical no la puede cortar nada más que en un punto. La representación de las superficies topográficas se basa en esta propiedad. Aprovechando esta característica, se proyectan los puntos de la superficie topográfica a la superficie de referencia, que en los casos más sencillos es el plano horizontal.
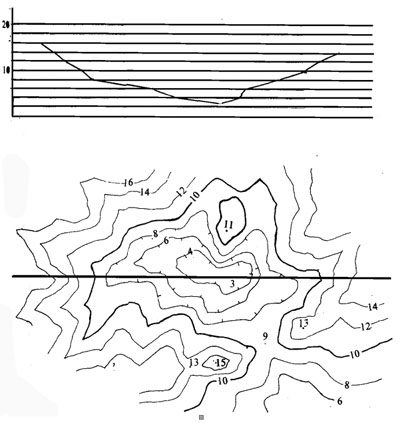
Las curvas de nivel o isohipsas son líneas que unen puntos de la superficie topográfica que presentan la misma altitud. O lo que es igual, la intersección de la superficie topográfica con un plano horizontal como muestra la figura 1
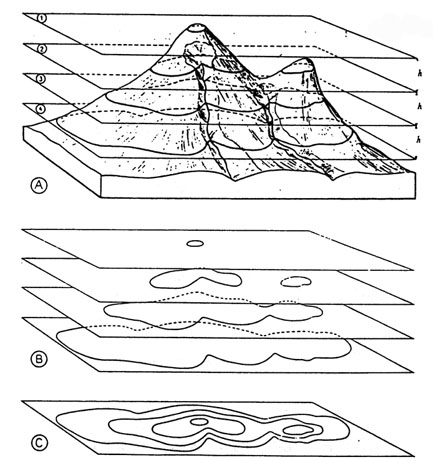
Figura 1. Relación entre el relieve y su representación mediante curvas de nivel. (Aubouin, Dercourt y Labasse, 1970)
Es importante tener claros los conceptos de desnivel y altitud, el primero tiene un origen arbitrario, mientras que la altitud está referida al nivel medio del mar (En España medido en el mareógrafo del puerto de Alicante) y se considera una medida absoluta. La figura 2 ilustra estos conceptos.
La equidistancia es la distancia constante entre dos planos de intersección o entre dos curvas de nivel. A escala 1:50.000 la equidistancia es de 20 metros. No debe confundirse la equidistancia, que hace referencia a medidas verticales, con la distancia sobre el plano entre dos curvas de nivel, que son medidas horizontales y que por lo tanto, estarán siempre a la escala del mapa.
Las curvas maestras son líneas de trazo más grueso y están separadas entre sí por una equidistancia constante, en el MTN a escala 1:50.000 la separación es de 100 metros de desnivel. Estas curvas están situadas entre las curvas normales, de trazo más fino. De esta manera, en el MTN 1:50.000 cada cuatro curvas normales habrá una quinta maestra
Las curvas de nivel suelen ser representadas de color siena. Por otra parte, pueden aparecer curvas auxiliares o intercalares que permiten precisar mejor la altura debido a su menor equidistancia; se representan con trazos finos discontinuos, que no tienen porqué cerrarse sino que se colocan donde se precisan y con la continuidad necesaria.
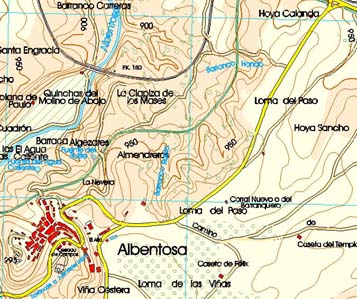
Figura 3. Mapa topográfico de Albentosa (Teruel), en el que observan las curvas de nivel que definen un valle y una zona plana
La representación topográfica de llanuras, elevaciones y depresiones
La clasificación primaria de las formas del terreno permite distinguir estos tres grupos de zonas. Las llanuras no lo son nunca exactamente, siempre hay alguna curva de nivel; es decir, existe una pendiente mínima.
En las zonas de elevación más elementales el terreno se halla por encima de una llanura; las curvas de nivel son cerradas y cada una envuelve a otra de cota mayor. En los casos análogos de depresiones el terreno está por debajo de una llanura; las isohipsas son cerradas también, pero envuelve cada una a otra de cota menor.
Más generalmente se puede hablar de una zona de elevación cuando a partir de una curva dada se cumple lo dicho antes (curva envuelta de mayor cota) y la zona está en depresión cuando sucede lo contrario.
En las condiciones de erosión más habituales son mucho más frecuentes las primeras, pero no debe descartarse la presencia de depresiones cerradas denominadas simas o torcas, por ejemplo en terrenos calizos y yesosos.
Divisorias, vaguadas y laderas
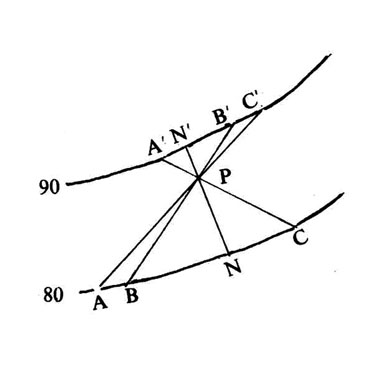
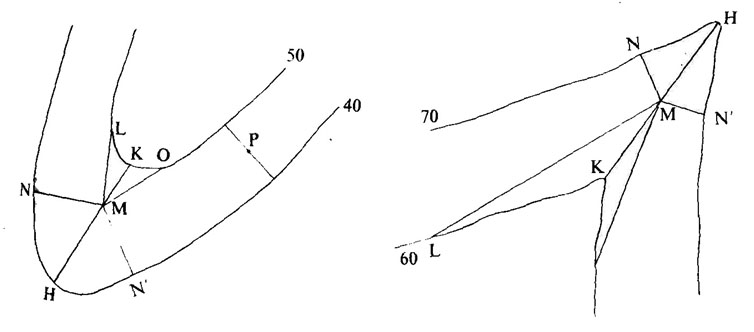
Generalmente al hallar la máxima pendiente en un punto P del terreno, se obtiene un segmento PN más corto que los demás (PA, PB, etc.) que resultan de unir P con puntos de la curva de nivel situada inmediatamente debajo y tales que el recorrido se haga siempre descendiendo: este segmento PN marca la línea de máxima pendiente hacia abajo.
Si se repite la operación con puntos de la curva inmediatamente superior se obtiene otra dirección PN’ (menor que PA’, PB’, etc.) que es la de máxima diente hacia arriba. PN y PN’ están prácticamente en una recta, salvo excepciones de terrenos especiales. En este caso se dice que P es un punto de ladera.
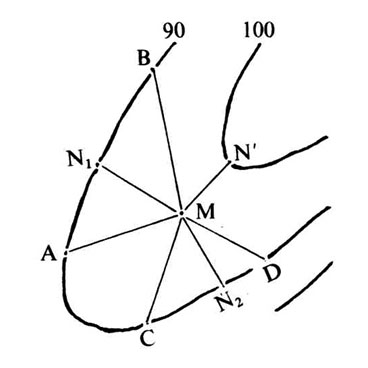
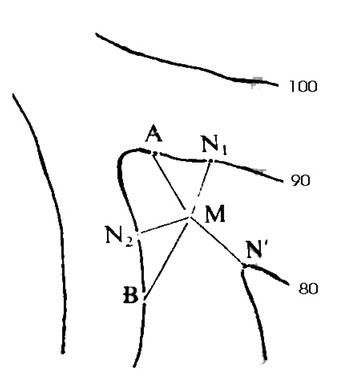
Pero puede ocurrir que haya dos soluciones MN1 y MN2 de máxima pendiente bajando al hacer la construcción en ciertos puntos M, aunque sus valores serán generalmente distintos; por el contrario, para el punto M hay una sola MN’, línea de máxima pendiente hacia arriba. Se da este caso cuando hay dos laderas que se cortan en M; este punto y otros próximos a él que tienen la misma propiedad se unen formando una línea más o menos recta llamada «divisoria». Se refiere este término a la divisoria de aguas, ya que las de lluvia discurren por la línea de máxima pendiente y por lo tanto las que caen en los puntos M pueden seguir una u otra ladera.
Por el contrario, puede ocurrir que haya dos máximas pendientes MN1 y MN2 subiendo y una sola bajando (figura); en este caso hay dos laderas que se cortan en M, que será uno de los puntos más bajos, y lo mismo ocurrirá con otros puntos cercanos a M que gocen de la misma propiedad. La alineación de estos puntos formará una curva, bastante rectilínea, llamada «vaguada». Las aguas que caen en las laderas discurren hasta la vaguada y continúan descendiendo por ella.
En el caso de la divisoria, el segmento que une M al punto más alejado H de la curva inferior cae dentro del ángulo NMN’; mientras que el que une con el punto más próximo K de la curva superior es el de mayor pendiente en dicho ángulo. Ambos segmentos, que tienen pendientes semejantes, llevan aproximadamente la dirección de la línea divisoria y por esto suele decirse que la divisoria es la línea de máxima pendiente subiendo y mínima bajando, expresión correcta si se precisa “partiendo un punto de ella misma” y con las restricciones de ángulos antes indicadas.
Análogamente, en una vaguada el segmento HM al punto más alejado de la curva superior es el de menor pendiente dentro del ángulo NMN’ y el KM (a la curva inferior) es el de mayor pendiente entre los que parten de M; se dice, similarmente, que la vaguada es la línea de mínima pendiente subiendo y máxima pendiente bajando, con las mismas observaciones que en el caso anterior.
Como los puntos H y K son los de mayor curvatura de las respectivas curvas y como se ve que cumplen con la misma condición que M, puede añadirse que las divisorias y las vaguadas pasan por los puntos de mayor curvatura de las isohipsas; en las divisorias el punto está envuelto por una curva de menor cota y en las vaguadas por otra curva de mayor cota.
Cumbres simas y collados
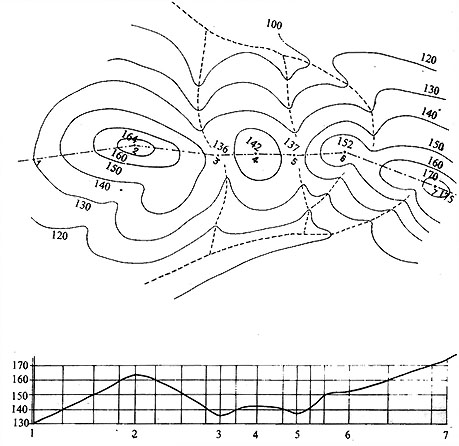
EI perfil de una divisoria resulta tener máximos y mínimos relativos, correspondientes a puntos en que la tangente es horizontal; los máximos, puntos más altos, se denominan “cumbres” (o cimas, picos, etc.) y los mínimos “collados”.
En el perfil de una vaguada, teóricamente se encontrarían también máximos y mínimos relativos; los mínimos serían los puntos más hondos, que pueden llamarse “simas” o fondos, sumideros, etc., y los máximos volverían a dar los “collados”. Pero los terrenos, sometidos generalmente a la erosión de las aguas de lluvia, suelen presentar vaguadas cuyo perfil es siempre descendente. La unión de dos vaguadas de distinta ladera en su parte más alta puede dar los collados (puntos 3 y 5 de la figura 9). Las “simas” sólo aparecen en las depresiones cerradas.
Todos estos puntos (cumbres, simas, collados) deben aparecer en los mapas con cota bien definida y deben ser situados al hacer el levantamiento topográfico. Entre las cumbres conviene destacar los máximos absolutos que son los picos más altos de la zona y siempre deben acotarse. En un collado se atraviesa la divisoria por un punto relativamente bajo; tales puntos son empleados por las vías de comunicación (carreteras, caminos, sendas) y reciben el nombre de “puertos” en este caso.
Los collados tienen la propiedad de que en ellos hay un punto común a dos curvas de nivel, aunque generalmente este punto no es de cota redonda y por lo tanto no está dibujada la curva correspondiente.
Los modelos digitales del terreno
En la actualidad, la representación del relieve se realiza mediante la generación de modelos digitales del terreno. Estos modelos pueden representar múltiples aspectos de una superficie topográfica, como la pendiente, la orientación o la rugosidad del terreno, sin embargo el modelo digital del terreno más utilizado es el modelo digital de elevaciones. Este modelo es una modelización matemática del relieve de una determinada zona.
De acuerdo con esta definición, un modelo digital de elevaciones (MDE) se define como una estructura numérica de datos que representa la distribución espacial de la altitud de la superficie del terreno. Un MDE puede formularse de forma genérica del modo siguiente:
z = F (x, y)
donde z es la cota del punto situado en las coordenadas planimétricas x e y, y F es la función que relaciona la variable con su localización geográfica. Los valores de x e y suelen venir referidos a un sistema de coordenadas plano, habitualmente un sistema de proyección cartográfica. En el caso europeo el sistema de proyección UTM y el sistema de referencia geodésico ETRS89.

Figura 9. Representación topográfica del término municipal de Olba (Teruel) mediante un modelo digital de elevaciones vectorial
La expresión anterior representa una superficie o campo escalar en la que la cota topográfica altimétrica es una variable continua. Dado que esta superficie topográfica está formada por un número infinito de puntos no es posible su modelización sin cierta pérdida en la información, tarea similar a la de la generalización cartográfica.
Digitalmente, sería factible presentar de forma explícita la ecuación anterior, que relaciona la altitud con su geolocalización. Sin embargo, la gran complejidad del relieve hace que su representación matemática mediante funciones sea inviable. En la práctica, las altitudes correspondientes a un área sólo pueden representarse mediante una ecuación cuando la superficie es pequeña y el relieve muy simple.
Para solucionar este inconveniente, se han buscado alternativas para representar la altitud mediante conjuntos limitados de datos topográficos, buscando un equilibrio entre la simplificación y la descripción realista del relieve.
Históricamente, los modelos digitales se han dividido en dos grupos en función de la representación de los datos: vectorial y raster. Los modelos vectoriales están basados en puntos y líneas definidas por sus coordenadas. En los modelos raster, los datos se interpretan como el valor medio de unidades elementales de superficie que dividen el terreno con una distribución regular, sin solapamiento y con recubrimiento total de la zona modelada.
En los modelos vectoriales los el terreno se representa a través de mediante líneas y puntos acotados. Los puntos se describen mediante dos coordenadas y las líneas, mediante dos puntos, el inicio y el final.
Figura 11. Mapa de pendientes, mapa de orientaciones y modelo digital acoplado a ortofoto. Realizado con un Modelo Digital de Elevaciones raster de una zona al oeste de Titaguas
Actualmente, los modelos más representativos son básicamente cuatro, de los cuales dos de ellos son vectoriales: isopletas o contornos y de red irregular de triángulos (TIN, triangulated irregular network); los otros dos son raster: matrices regulares y matrices jerárquicas escalables. En Topografía, el modelo más utilizado es el de redes de triángulos irregulares (TIN). En esta estructura, los triángulos se construyen ajustando un plano a tres puntos cercanos no colineales, formando un mosaico que se adapta a la superficie con diferente grado de detalle, en función de la complejidad del relieve. Para realizar una buena modelización con este tipo de MDE, es necesario representar las líneas de rotura del terreno: cabezas y pies de talud, vaguadas, divisorias y los puntos de cima o depresión.