Con la entrada en vigor de la Ley 13/2015, de 24 de junio, de Reforma de la Ley Hipotecaria, se han introducido por primera vez en la legislación que afecta a la delimitación de la propiedad inmobiliaria, conceptos que para algunos técnicos pueden resultar novedosos, aunque realmente no lo son. Nos referimos a las coordenadas georreferenciadas.
Con esta ley en vigor, imponiendo en muchos casos la obligatoriedad de adjuntar las coordenadas georreferenciadas de los vértices de los inmuebles, podemos preguntarnos ¿qué ventaja ofrece? ¿realmente tiene sentido exigir la georreferenciación de los vértices de los inmuebles? Evidentemente, lo tiene. La gran ventaja que ofrece la georreferenciación es que nos define la posición de un punto (en este caso del límite de un derecho real) de manera unívoca, esto es, esas coordenadas no pueden pertenecer a otro punto y ese punto no puede tener otras coordenadas, siempre que trabajemos, como exige la ley, en el sistema de referencia oficial ETRS89 (European Terrestrial Reference System 1989), Sistema de Referencia Terrestre Europeo 1989, y en la proyección UTM (Universal Transverse Mercator), Universal Transversa de Mercator.
Con la tecnología disponible en la actualidad, obtener las coordenadas georreferenciadas de un vértice puede resultar una tarea sencilla pero, como sucede con gran parte de la tecnología utilizada comúnmente en nuestro día a día, detrás de ella hay una gran cantidad de conocimiento científico y un complejo desarrollo matemático que es imprescindible conocer para saber qué estamos haciendo en cada momento y sobre todo, para no convertirnos en meros “aprietabotones” de un equipo topográfico, sin tener ni idea del significado físico de los números que nos aparecen en la pantalla.
Actualmente, el uso de la topografía clásica ha quedado relegado por las técnicas GNSS a aquellas ocasiones en las que por motivos de visibilidad o cobertura, éstas no se pueden utilizar. Pero hay ocasiones en las que resulta imprescindible el uso de los métodos de topografía clásica y uno de los más utilizados es el método de poligonal, del que vamos a hablar en este artículo. Haremos una poligonal cuando necesitemos dotar de coordenadas georreferenciadas a varios puntos que puedan formar un itinerario, generalmente para realizar desde ellos una radiación. Para ello deberemos partir de al menos un punto de coordenadas y orientación conocidas.
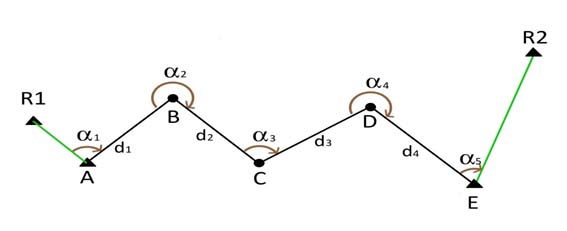
Una poligonal consiste en una serie de puntos unidos por tramos o ejes. El método topográfico de poligonación se basa en determinar las coordenadas de los mencionados puntos, a partir de la medición en campo de las longitudes de los ejes (distancias entre puntos consecutivos) y los ángulos entre ejes consecutivos. Para realizar estas mediciones se utiliza instrumental topográfico, que deberá estacionarse en todos los puntos que forman parte de la poligonal. De lo dicho se puede deducir que el método de poligonación consiste en unir los puntos (A, B, …, E en la Figura 1) que forman la poligonal, a partir de radiaciones encadenadas.
Figura 1. Esquema de una poligonal de cuatro ejes.
Los puntos A, B, C, D y E de la Figura 1 se llaman vértices (o estaciones, debido a que se “estaciona” el instrumental en ellos) y los segmentos AB, BC, CD y DE que se muestran en la Figura 1, se denominan ejes o tramos del itinerario. Dos ejes contiguos forman un ángulo (considerando también como eje las visuales de referencia) que también deberá ser medido, como ya se ha indicado.
La metodología de campo en el caso que ilustra la Figura 1 será la siguiente:
- Estacionamiento en A y toma de lecturas angulares, a la referencia R1 de coordenadas conocidas y a la estación siguiente B. Medición de la distancia .
- Estacionamiento en B y toma de lectura angular y distancia a la estación anterior A y a la estación siguiente C.
- …
- Estacionamiento en E y toma de lecturas angulares, a la referencia R2 de coordenadas conocidas y a la estación anterior D.
Con los datos obtenidos del procedimiento anterior, seremos capaces de obtener las distancias entre vértices y los ángulos α que forman los ejes.
La poligonal es un método de observaciones encadenadas, por lo que los errores se acumulan y se pondrán de manifiesto en la última estación, que deberá ser de coordenadas conocidas si queremos realizar una compensación.
Clasificación de las poligonales
Según el punto de inicio y fin de la poligonal, esta puede ser:
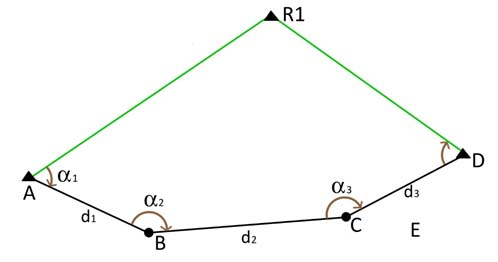
- Abierta, cuando la estación final es distinta de la estación inicial, como se muestra en la Figura 2
Figura 2. Poligonal abierta
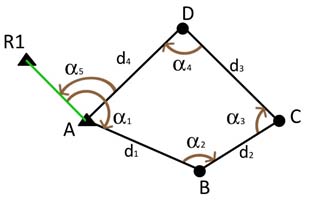
- Cerrada, si el itinerario comienza y termina en la misma estación, ya sea ésta de coordenadas conocidas o no, como se muestra en la Figura 3.
Por otro lado, dependiendo de si se conocen las coordenadas del punto de cierre (imprescindible para que se pueda realizar una compensación de los errores), la poligonal puede ser:
- Encuadrada, si se parte de un punto de coordenadas conocidas y se termina en otro punto de coordenadas conocidas también, ya sea distinto (abierta) o el mismo que el del inicio (cerrada).
- Colgada, si termina en una estación de coordenadas desconocidas.
Lógicamente, es recomendable realizar itinerarios encuadrados, ya que permiten detectar errores y si estos son asumibles, compensarlos.
Cálculo de la poligonal
Como ya se ha comentado, se necesita partir de unas coordenadas y orientación conocidas para el primer punto. Esto no quiere decir que, si se desea trabajar en coordenadas relativas, no se pueda dar unas coordenadas y orientación aleatorias al punto de partida y se pueda seguir trabajando, aunque este no es el caso que nos ocupa, ya que no estaremos georreferenciando.
Corrida de acimutes
La primera tarea a realizar será la corrida de acimutes. Partiendo del acimut del primer punto a la referencia, se calcularán el resto a partir de los ángulos entre ejes.
Para ello, se necesitará obviamente calcular los ángulos entre ejes, estos se calcularán simplemente como diferencia de lecturas. Se aconseja adoptar el sentido dextrógiro, esto es, el sentido de crecimiento de los ángulos, que nos permitirá calcular los acimutes siempre sumando el ángulo correspondiente.
Cálculo de coordenadas
Con los acimutes calculados y considerando que tenemos las distancias observadas en campo, estamos en disposición de calcular las coordenadas. Cabe señalar que se deberá obtener la distancia media de las medidas en campo.
Teniendo en cuenta que el instrumental actualmente utilizado nos proporciona directamente las distancias reducidas, trabajaremos con estas.
Si no fuese así, las podríamos obtener de las geométricas, a partir del ángulo vertical, con la fórmula
Conclusión
Como hemos visto de forma básica y sin entrar en detalle, no es baladí la formación técnica necesaria para llevar a cabo una georreferenciación cuando las condiciones no son las más favorables; pues aunque la tecnología nos lo pondrá fácil en la mayor parte de las ocasiones, cuando esto no es así, la ciencia y técnica que es necesario conocer es compleja y en muchas ocasiones el proceso no será sencillo ni inmediato.
Siempre será imprescindible comprender y diferenciar todas las metodologías e instrumental Topográfico y Geodésico disponible a la hora de delimitar con coordenadas georreferenciadas un inmueble o un derecho real: sistemas GNSS, estaciones totales, láser escáner, fotogrametría…. La metodología e instrumental a utilizar en cada caso dependerá de una gran variedad de factores, como la cobertura vegetal y constructiva del bien inmueble o la extensión y grado de precisión requerido. No será lo mismo georreferenciar una finca rústica de 100 hectáreas de secano, que un rascacielos en el centro de una ciudad. El método de poligonal nos ayudará cuando las condiciones no sean las más favorables y no haya más remedio que rescatar las técnicas clásicas que los Ingenieros en Topografía llevamos utilizando hace cientos de años, mucho antes de que aparecieran los drones y los sistemas GNSS. No es cierto, como dicen algunos, que hace cincuenta años la tecnología existente no permitiera georreferenciar con gran precisión, solo que era un poco más costoso …