Desde hace más de dos mil años se sabe que, sin tener en cuenta las montañas y los valles, la Tierra es aproximadamente esférica. Para la elaboración de algunos tipos de mapas fue, y aún sigue siendo válido pensar en la Tierra como una verdadera esfera, pero los mapas y planos topográficos que hoy en día se realizan cuidando al máximo la precisión, necesitan mayor exactitud a la hora de considerar la forma de la Tierra.
1. La forma de la Tierra
Los continentes y las montañas que se elevan por encima del nivel del mar representan irregularidades menores de la esfericidad de la Tierra y son bastante insignificantes con relación al tamaño de la Tierra, aunque no lo sean, desde luego, para los seres humanos. Incluso el achatamiento, es decir, la diferencia entre los radios polar y ecuatorial, que resultan de la rotación de la Tierra, es comparativamente poco importante. Si se redujera la Tierra al tamaño de un gran balón de 1 m de diámetro, el achatamiento polar alcanzaría menos de 3,5 mm, mientras que la montaña más alta apenas podría medirse sin instrumentos especiales y desde luego la mayoría de nosotros no la distinguiríamos.
La Tierra se puede considerar esférica en una primera aproximación, pero se necesita ir más allá para elaborar cartografía y planos topográficos
A pesar de que las desviaciones de la forma de la Tierra respecto a la esfera perfecta son relativamente muy pequeñas, son importantes en el proceso de elaboración de los mapas topográficos, ya que afectan a las observaciones de los topógrafos y a la precisión con que sus datos pueden transferirse a la cartografía.
El encuadre topográfico en que se basan todos los mapas requiere de la transferencia sistemática de las relaciones geométricas observadas sobre la superficie esférica de la Tierra a la superficie plana del mapa. Varios son los factores a considerar. Primero, la distribución irregular de la masa terrestre afecta a la dirección de la gravedad, que determina la horizontalidad y la verticalidad de cada lugar de las cuales dependen muchas observaciones locales. La forma de esferoide irregular que considera las anomalías de la gravedad se denomina geoide. Segundo, para la elaboración de mapas topográficos, las observaciones realizadas sobre el geoide deberán transferirse a una superficie de referencia geométrica regular, denominada elipsoide, que incorpora el achatamiento y se aproxima muchísimo al geoide. En tercer lugar, las relaciones geográficas tridimensionales del elipsoide deberán transformarse al plano bidimensional del mapa por medio de diversos procedimientos denominados proyecciones cartográficas. La determinación de las adecuadas características del geoide y los elipsoides concierne al campo de la Geodesia. Seguidamente ofreceremos una breve descripción del geoide y del elipsoide.
2.- El geoide
El geoide es la forma que aproximadamente tendría el nivel medio del mar actual y el nivel del agua de una serie de canales surcando la Tierra a nivel del mar. Se define técnicamente como una superficie equipotencial, es decir, aquella donde la dirección de la gravedad es perpendicular en todos los lugares. Debido a variaciones en la distribución de las masas continentales y en la densidad de los componentes de la Tierra, el geoide normalmente asciende en los continentes y desciende en las áreas ocupadas por los océanos. Tiene también otras protuberancias y depresiones que difieren de la «uniformidad media» y que pueden llegar hasta los 60 m. El geoide es un factor muy importante en la Topografía y sobre todo, en la Cartografía, ya que todas las observaciones sobre la Tierra se realizan, claro está, sobre el geoide. Como el geoide es irregular y por lo tanto la dirección de la gravedad no se dirige desde todos los puntos hacia el centro de la Tierra, es necesario corregir las desviaciones de la vertical de modo que las medidas de las distancias sobre la superficie concuerden con las determinadas mediante observación astronómica.
3.- El elipsoide
El geoide está también deformado por la rotación de la Tierra. A causa de que gira sobre un eje, el geoide bombea un poco en la región ecuatorial y se achata en las regiones polares. La sección que atraviesa los polos es elíptica. El grado real de achatamiento es de unos 21,5 km, diferencia entre los radios polar y ecuatorial; evidentemente el radio ecuatorial es el mayor.
Para elaborar los mapas topográficos con precisión deberá utilizarse una superficie de referencia geométrica regular. Las observaciones sobre el geoide se transfieren a la figura regular que más se aproxima a él. Ésta es un elipsoide de revolución, es decir, una figura producida por una elipse que gira alrededor de su eje menor.
Debido al achatamiento de la Tierra, la sección más plana del geoide está situada en el sector polar y la de mayor curvatura se sitúa en el ecuador. A causa de que una gran parte de la navegación se basa en el ángulo formado por algún cuerpo celeste y el plano horizontal, surjen complicaciones al desviarnos de la verdadera esfera. Por eso, cuando se prepara cartografía para su uso en navegación o para la determinación o trazado de rumbos y distancias precisos de un lugar a otro, es necesario tener en cuenta el achatamiento. En la mayoría de los casos de mapas topográficos a pequeña escala, esto puedo ignorarse tranquilamente.
En enero de 2015 entró en vigor la ley por la que se sustituyó el elipsoide oficial que se venía utilizando en España, el elipsoide de Hayford, por el elipsoide GRS80, de utilización en toda Europa.
4.- Sistemas de Coordenadas
La localización relativa de unos puntos respecto a otros requiere la utilización de los conceptos de dirección y distancia. Estos puntos se han de apoyar en algún sistema; los pueblos primitivos lo hicieron probablemente de un modo relativo, utilizando ayudas tales como las direcciones de la salida y la puesta del sol, adelante y atrás, izquierda y derecha, etc., y probablemente expresaron distancias en términos de tiempos de desplazamiento.
Actualmente existen dos sistemas de uso general. El más antiguo, el sistema de coordenadas geográficas que utiliza la latitud y la longitud, fue utilizado por primera vez por los geógrafos-filósofos griegos, antes del comienzo de la era cristiana. Es éste el sistema principal, ya que se utiliza para todos los cálculos de localizaciones básicas, como en navegación y en Cartografía.
El segundo sistema, denominado de coordenadas rectangulares planas, o simplemente de coordenadas planas, es también antiguo, por lo menos en su forma básica. Fue un elemento común de la Cartografía china tras su inclusión en los seis principios de la elaboración de mapas enunciados por Pei Hsiu en el siglo tercero de nuestra era. Modernamente, el sistema de coordenadas planas evolucionó a partir de las coordenadas cartesianas aplicadas a necesidades topográficas, pero también ha sido muy útil para otros usos.
4.1.- Coordenadas geográficas
En una superficie esférica inmóvil no existiría punto de partida natural, pero la Tierra gira sobre su eje y revoluciona alrededor del Sol de un modo regular. Debido a que de este modo, pueden predecirse las posiciones del resto de los cuerpos celestes, la posición de un sujeto puede calcularse si éste posee algún modo de conocer el tiempo y una efemérides, almanaque astronómico que contiene tablas formadas por la posición diaria aparente de los cuerpos celestes. El sistema de coordenadas geográficas fue ideado para posibilitar el establecimiento de una localización. Los dos polos, donde el eje de rotación intersecta la superficie de la Tierra, proporcionan los puntos en que se basa el sistema. La formulación de una localización sobre la Tierra requiere la determinación de la distancia Norte-Sur, llamada latitud, y la distancia Este-Oeste, denominada longitud.
Latitud φ
El sistema de hallar la propia situación en una posición norte-sur depende de la curvatura regular de la superficie terrestre. La latitud de un punto dado puede definirse como el ángulo formado por una línea perpendicular a la superficie y el plano del ecuador en dicho lugar. Esto se realiza observando la altitud (ángulo por encima del horizonte) de algún cuerpo celeste y seguidamente, con la ayuda de los datos que figuran en una efemérides, calculando el ángulo deseado en la dirección Norte-Sur. Debido a la forma esférica de la Tierra, el cambio de posición a lo largo de una línea Norte-Sur se ve acompañada por un cambio en la elevación angular de los cuerpos celestes en relación al plano horizontal de la Tierra. Cuando los cuerpos celestes se hallan en el plano del arco, como por ejemplo la estrella Polar o el Sol al mediodía, existe una relación de uno a uno; es decir, por cada grado de distancia a lo largo de un arco de Norte a Sur, la elevación sobre el horizonte del cuerpo cambiará en 1º. Puede observarse cualquier estrella, y pueden realizarse las correcciones adecuadas para obtener el correspondiente ángulo cenital.
Ello simplifica algo el problema, debido a que la Tierra gira alrededor de su eje, y la mayoría de los cuerpos celestes parecen moverse mientras el observador es desplazado de un lugar a otro. El hecho fundamental es, sin embargo, que la posición Norte-Sur puede determinarse midiendo el ángulo vertical existente entre la horizontal y un cuerpo celeste.
Era natural utilizar esta relación para un sistema de coordenadas esféricas. Los antiguos imaginaron la existencia de un número infinito de círculos alrededor de la Tierra, paralelos entre sí. El círculo que dividía la Tierra en dos mitades, equidistantes a los polos, se llamó, Ecuador. Las líneas situadas al Norte del ecuador se denominan de latitud Norte, y las situadas al Sur, de latitud Sur.
Longitud λ
Mediante la latitud se establece únicamente la posición Norte-Sur de la Tierra. El componente transversal, longitud o distancia Este-Oeste, viene proporcionado por infinidad de círculos máximos denominados meridianos. A diferencia del Ecuador, en el sistema de latitud, ningún meridiano tiene una base natural para ser la línea de arranque a partir de la que pueda calcularse la distancia Este-Oeste en grados, minutos, y segundos de longitud. En el sistema de latitud, a partir de un meridiano dado, seleccionado como línea de partida, se determina la posición Este-Oeste, mediante la distancia angular a lo largo de un círculo paralelo.
A mediados del siglo dieciocho, sólo podía calcularse con una cierta precisión la latitud. La distancia Este y Oeste depende de diferencias de tiempo y, para facilitar el cálculo, se requiere el conocimiento de la hora del día simultáneamente en los dos lugares. Sin la ayuda de relojes muy exactos que puedan transportarse o de unas comunicaciones instantáneas, ello únicamente puede llevarse a cabo mediante observaciones astronómicas y cálculos muy elaborados. A través de los años el resultado había presentado un considerable error en las ubicaciones Este-Oeste, cosa que provocó el glorioso error del siglo quince. La creencia de que la distancia desde Europa en dirección Oeste hasta Asia era menor que la mitad de lo que en realidad es.
Cuando la determinación precisa de la longitud llegó a ser esencial para la navegación, se ofrecieron generosos premios a quien fuera capaz de hallar una solución. Surgieron una gran variedad de métodos, que abarcaban desde las observaciones de un reloj celeste, o el comportamiento de los satélites de Júpiter, hasta la utilización de las variaciones (declinaciones) de la brújula. Cuando Harrison desarrolló el cronómetro, a mediados del siglo XVIII, se solucionó el problema.
Debido a que todos los paralelos son círculos concéntricos y giran todos a la misma velocidad angular (360º diarios), contando con un reloj que indique con exactitud la hora solar que se registra en otro lugar, la diferencia entre esta hora y la hora solar local en horas, minutos y segundos, puede convertirse en la diferencia en longitud entre los dos puntos mediante cálculos matemáticos. Esta operación se realiza actualmente mediante señales horarias radiadas a intervalos regulares, así como mediante la utilización de cronómetros.
Los meridianos son semejantes entre sí, y cualquiera de ellos podría elegirse como meridiano de origen a partir del que podría comenzarse la numeración de la longitud. La elección se convirtió, como puede imaginarse, en un problema internacional. Numerosos países, todos con ambiciones patrióticas, deseaban tener la longitud 0 en el interior de sus fronteras o como meridiano de su capital. Durante muchos años cada estado publicó sus propios mapas topográficos y cartas cuyas longitudes se calculaban a partir de su particular meridiano de origen. El resultado fue una gran confusión.
Durante el último siglo, muchos estados comenzaron a aceptar el meridiano del observatorio de Greenwich cerca de Londres, como 0 y, en 1884, fue ratificado como tal en una conferencia internacional. Actualmente se ha aceptado plenamente como meridiano de origen, pero algunos mapas topográficos muestran todavía dos tipos de meridianos, uno de ellos basa su numeración en un meridiano local y el otro en el sistema de Greenwich.
4.2. Coordenadas rectangulares
Sobre una superficie plana sin límite no existe punto de referencia natural; es decir, cada punto es igual a los demás. Un sistema arbitrario de situación sobre la superficie de un plano ha venido siendo utilizado durante mucho tiempo, estableciendo un «punto de origen» en la intersección de dos «ejes» perpendiculares, convenientemente localizados. El plano es dividido en una cuadrícula mediante un número infinito de líneas separadas por espacios iguales, paralelas a cada eje. La posición de cualquier punto sobre el plano con referencia al punto de origen puede indicarse señalando la distancia desde cada eje hasta el punto, medido en cada caso en paralelo al otro eje, y expresado con la precisión deseada. En el sistema de coordenadas rectangulares (por ejemplo, papel cuadriculado), la distancia «horizontal» se denomina coordenada X o abscisa, y la distancia perpendicular a éste se denomina coordenada Y u ordenada.
El sistema de coordenadas geográficas es muy útil para grandes superficies, y la medición angular de distancias y direcciones, expresada en grados, minutos y segundos, apenas puede ser mejorada. Pero a menudo resulta incómoda. El mayor alcance de la artillería durante la Primera Guerra Mundial, hizo cada vez más difícil conseguir un acimut (rumbo o dirección) y alcance (distancia) precisos. Para simplificar el problema, los franceses construyeron sobre sus mapas cuadrículas de coordenadas rectangulares. Como las fórmulas de la geometría plana son mucho más sencillas que las de la geometría esférica, otros estados prontamente siguieron este método y, en el período de entreguerras, se diseñaron un buen número de sistemas de coordenadas planimétricas rectangulares. Puede decirse que actualmente la utilización de sistemas de cuadrícula es prácticamente universal.
Figura 3.4 . Sistema de coordenadas cartesiano.
El procedimiento básico es el siguiente: en primer lugar, se elabora un mapa topográfico, transformando la superficie esférica en un plano (mediante un sistema de proyección cartográfica), y una vez preparado el mapa plano, se le superpone, una cuadrícula de coordenadas regulares planas. Los dos conjuntos de líneas rectas y paralelas están colocados a igual distancia, perpendiculares unos a otros. Para localizar una posición únicamente es preciso especificar las coordenadas X e Y al nivel de precisión que se desee en la división decimal de las unidades de distancias terrestres. Ello es mucho más sencillo que utilizar grados, minutos y segundos de latitud y longitud.
Para simplificar el cálculo de posición, únicamente se utiliza la parte superior derecha de un sistema de coordenadas planas, de modo que ambos conjuntos de coordenadas sean positivos, y por lo tanto no exista repetición de los números al Este y al Oeste, al Norte y al Sur de los ejes. Normalmente, el origen de la numeración se sitúa fuera de la superficie del mapa, en la parte inferior izquierda.
La referencia de la cuadrícula se lee del mismo modo como localiza un punto sobre un papel cuadriculado. En las coordenadas topográficas rectangulares, siempre se índica primero el valor X o abscisa; luego el valor Y u ordenada. Como norma, cuando se utilicen referencias de cuadrícula, estas deben siempre «leerse hacia la derecha y hacia arriba».
Normalmente, las coordenadas de la proyección se utilizan únicamente en mapas topográficos a gran escala, ya que las distorsiones que resultan de la transformación de la superficie esférica a un plano convierten a los mapas de pequeña escala en poco aconsejables para realizar cálculos y referencias detalladas. La mayoría de los mapas topográficos a gran escala presentan uno o más sistemas de coordenadas planas, y algunos territorios han adoptado un sistema estatal de coordenadas planas.
Una característica importante de un sistema de coordenadas planas es el modo en que están organizados los factores de la escala. Depende del sistema de proyección del mapa. En los primeros años de este siglo, se utilizaron diversos tipos de proyecciones para los sistemas de coordenadas planas, pero actualmente la mayoría de dichos sistemas se basan únicamente en tres proyecciones cartográficas: la de Mercator transversa, la estereográfica polar y la cónica conforme de Lambert. Nosotros nos centraremos en la primera, oficial en toda Europa, conocida como U.T.M..
5.- La proyección UTM
A pesar de que algunos países hayan desarrollado sistemas particulares útiles para sus necesidades, el sistema de cuadrícula Universal Transversa de Mercator (UTM) es el comúnmente utilizado. Este sistema de reticulado y la proyección en que se basa ha sido adoptado para mapas topográficos, referencias de imágenes de satélite, bases de datos de recursos naturales y otras aplicaciones que requieren localizaciones precisas.
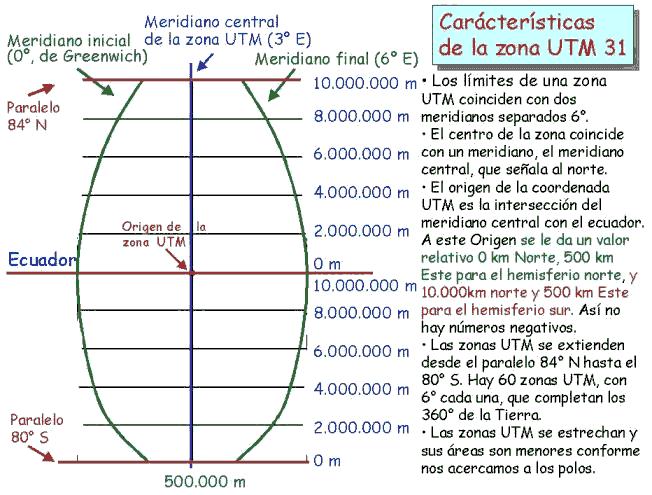
En el sistema de cuadrícula UTM, la superficie terrestre comprendida entre latitudes 84ºN y 80ºS ha sido dividida en columnas Norte-Sur de un ancho de 6º de longitud, llamadas zonas. Se numeran de 1 a 60 hacia el Este, empezando en el meridiano 180º. Cada columna es dividida en cuadriláteros de una altura de 8º de latitud. Las hileras de cuadriláteros tienen asignadas letras consecutivas de la C a la X (omitiendo la I y la O), empezando en los 80º latitud S. La hilera X tiene 120 de latitud, extendiéndose desde los 72ºN a los 84ºN para cubrir todas las zonas de tierra del hemisferio Norte. Cada cuadrilátero tiene asignado una combinación número-letra. Como siempre, en una red de referencia se lee hacia arriba y hacia la derecha. Cada cuadrilátero es dividido en cuadrados de 100.000 m designados mediante un sistema de combinación de letras.
La línea central de una zona UTM siempre se hace coincidir con un meridiano del sistema geodésico tradicional, al que se llama meridiano central. Este meridiano central define el origen de la zona UTM.
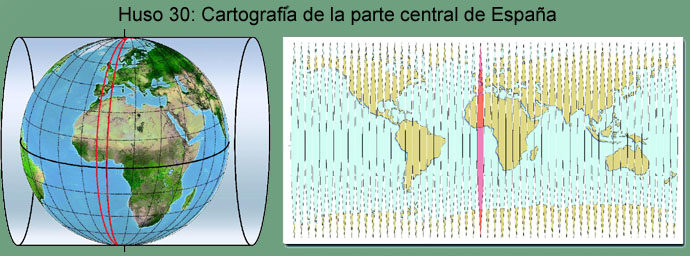
Esquema explicativo de la representación topográfica de la parte central de España en la proyección UTM
Dentro de cada zona, el meridiano central de la zona toma un valor de 500.000 m Este. El ecuador es asignado como teniendo un valor de O m Norte para el hemisferio Norte y un valor arbitrario de 10 millones de m Norte para el hemisferio Sur.
Para la red UTM es empleada la proyección transversa de Mercator, por lo que a lo largo de cualquier línea Norte-Sur de la cuadrícula (sólo la línea central de la cuadrícula de cada zona es un meridiano) el factor de escala es constante, pero varía en dirección Este-Oeste. A lo largo de la línea central de la cuadrícula de cada zona de la red UTM, el factor de escala es de 0,99960 (escala menor), y en los márgenes de la parte más ancha de la columna (en el Ecuador) a unos 363 km de distancia del centro, el factor es de 1,00158.
A continuación se presenta un esquema de un huso, este esquema no está dibujado a escala. La altura de una zona UTM es 20 veces la distancia cubierta por la escala horizontal. Se ha dibujado así por razones de espacio.